|
|
本帖最后由 seven_nana 于 2017-7-17 13:23 编辑
美德两国针对多层装甲体系的免疫区计算方式
本帖内容未经允许不得转载
美国海军的算法
注：以下算法中，第一种只能说是参考书中记载的算法，尚无法确认是否为官方算法；而第二种是基于免疫区数据，运用官方的穿深曲线及穿深计算方法反推的，虽然后两者是官方的，但前者尚无法确认是否为官方数据。
正推算法
根据Robert F. Sumrall的Iowa Class Battleships: Their Design, Weapons and Equipment：
当两层装甲间隔布置时，其等效厚度可按上层*0.5+下层来计算；而当两层装甲叠加时，其等效厚度可按厚度较大的那层+厚度较薄那层*0.7来大致估算。
衣阿华级的水平防护，是1.5英寸的露天甲板，外加4.75英寸的装甲甲板及1.25英寸的背板，按上述算法，等效6.375英寸。
反推算法
根据Norman Friedman的U.S. Battleships - An Illustrated Design History：
面对16英寸/45倍经火炮发射的2,700磅穿甲弹，衣阿华级的免疫区为20,200-25,500码；而面对16英寸/50倍经火炮发射的2,700磅穿甲弹，衣阿华级的免疫区为23,600-27,400码。
在25,500码距离上，16英寸/45倍经火炮发射的2,700磅穿甲弹，落角为26.20度，着速为1,514英尺/秒，按照经验式（Ord. Sk. 78841）计算值，可以击穿5.92英寸的水平装甲。
在27,400码距离上，16英寸/50倍经火炮发射的2,700磅穿甲弹，落角为24.42度，着速为1,595英尺/秒，按照经验式（Ord. Sk. 78841）计算值，可以击穿5.85英寸的水平装甲。
根据Norman Friedman的U.S. Naval Weapons中摘录的1942年的官方穿深曲线：
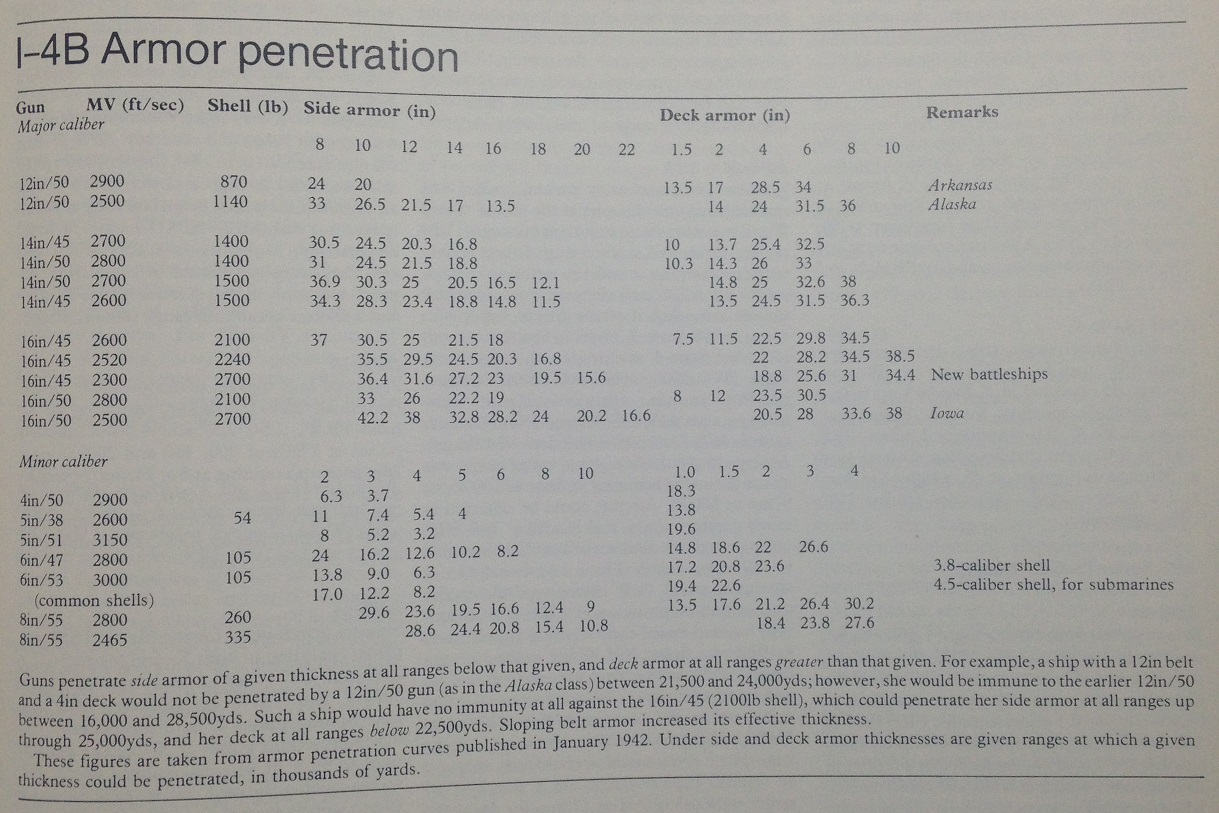
16英寸/45倍经火炮发射2,700磅穿甲弹，可在25,600码距离上击穿6英寸的水平装甲；而16英寸/50倍经火炮发射2,700磅穿甲弹，可在28,000码距离上击穿6英寸的水平装甲；这两组数据与经验式计算值相当接近。
数据对比
基于免疫区数据反推出的装甲厚度，与根据Sumrall书中记载的正推算法求得的等效厚度，存在一定出入。
德国海军的算法
先前我在德国海军的装甲防护设计理念中已经明确说明，德国海军在处理多层装甲体系时，是按照总击穿速度的平方等于击穿各层装甲所需速度平方之和来计算的，且不考虑入射角度的变化以及被帽脱落造成的影响。
下面我将结合德国海军官方所估算的俾斯麦级对抗英国15英寸舰炮时的免疫区来演示具体算法。
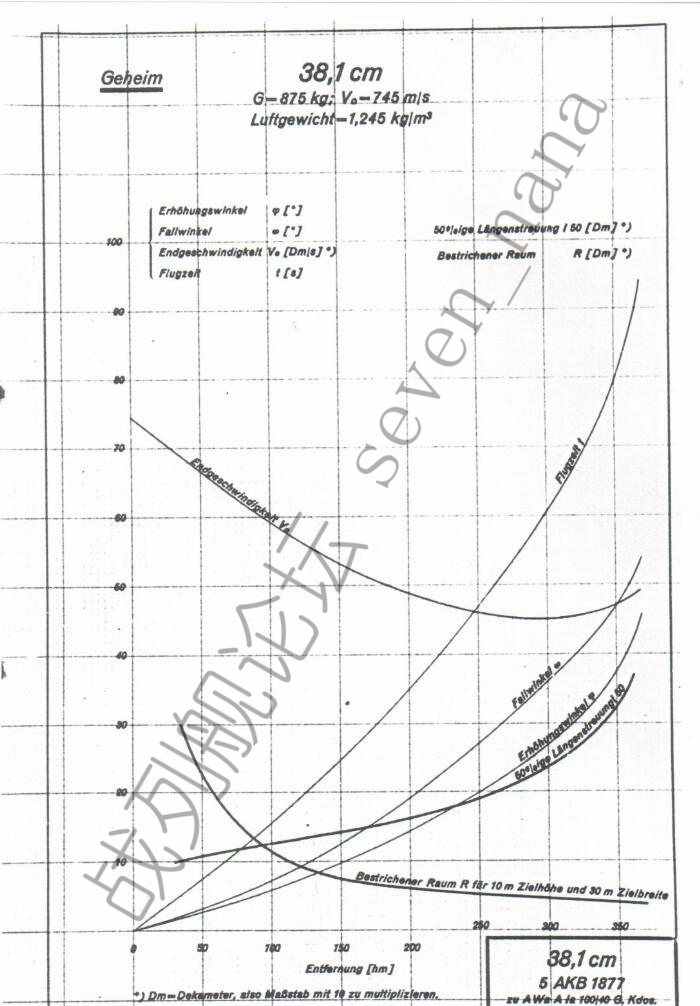
这是德国海军所估算的英国15英寸舰炮的射表：
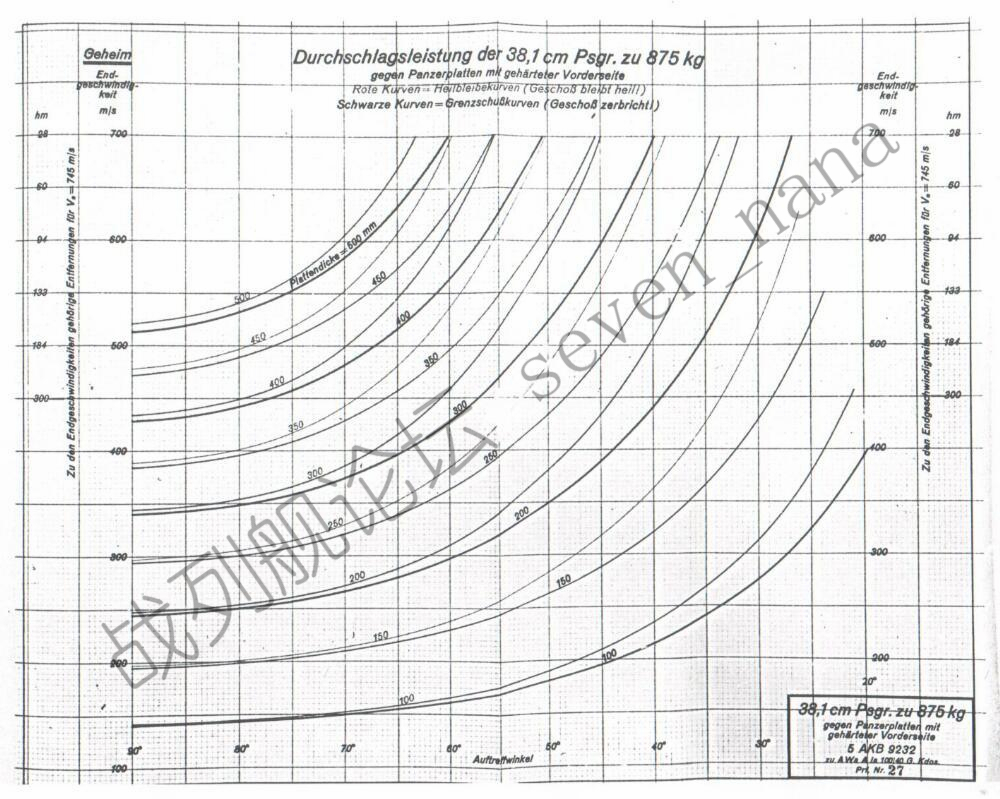
这是德国海军所估算的英国15英寸穿甲弹对表面硬化装甲的穿深曲线：
浅色线（原始图表中为红线）为完整穿透状态下的曲线，深色线（原始图表中为黑线）为不完整穿透状态下的曲线
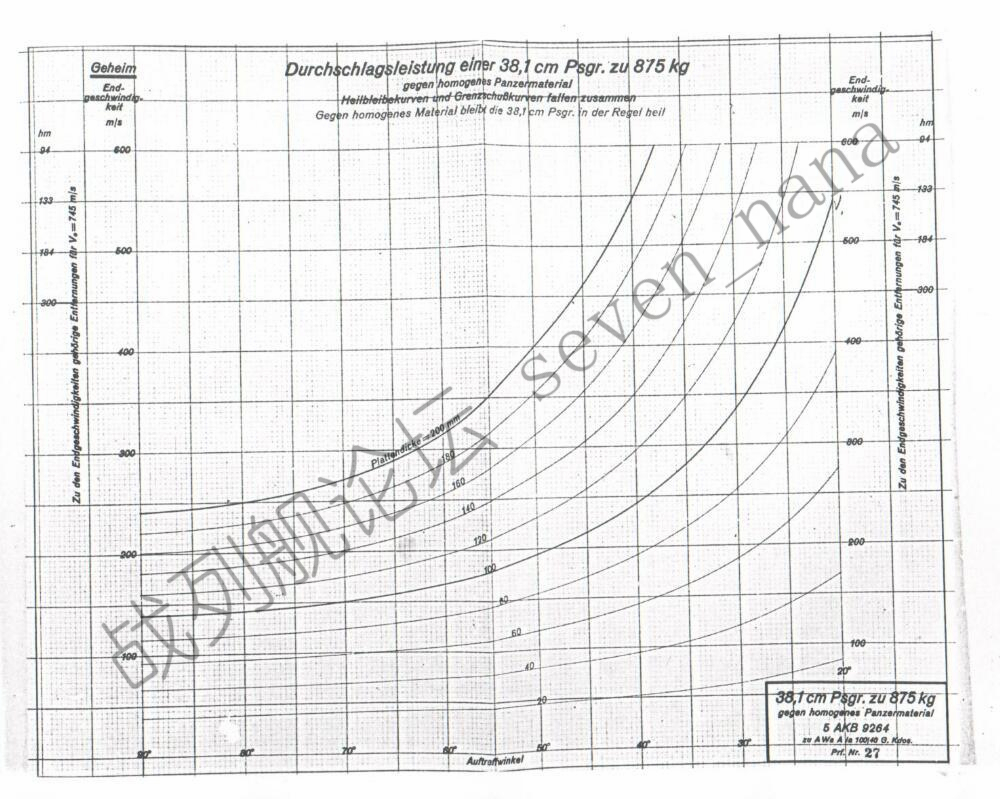
这是德国海军所估算的英国15英寸穿甲弹对均质装甲的穿深曲线：
完整穿透状态下的曲线与不完整穿透状态下的曲线实际上是重合的，因此图中仅有一条曲线
这是德国海军所估算的俾斯麦级对抗英国15英寸舰炮时的免疫区：
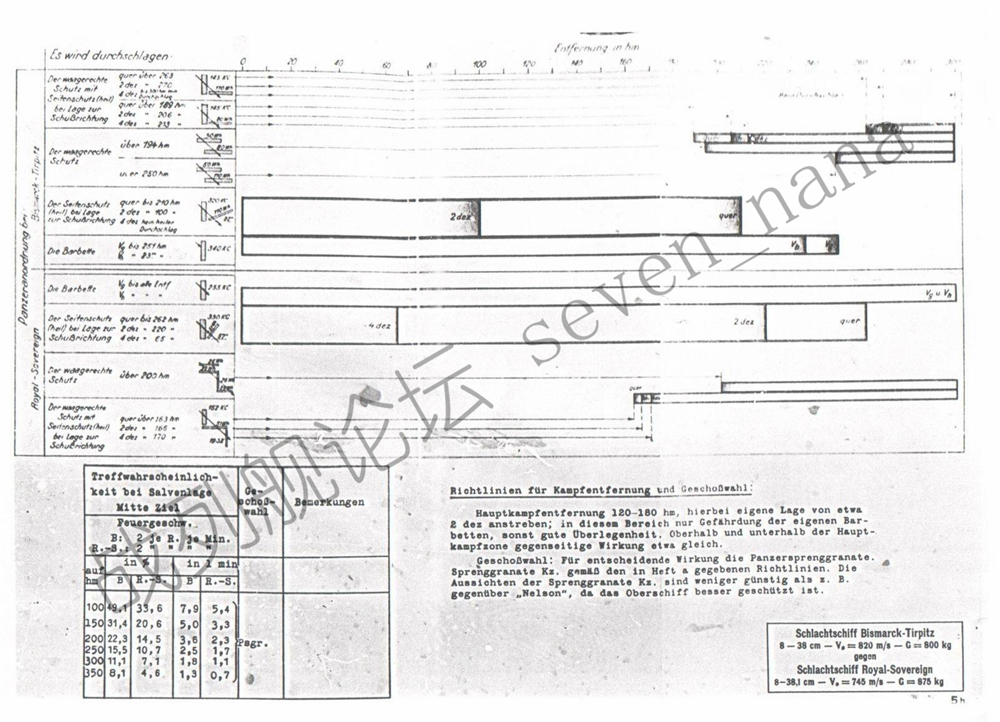
| 俾斯麦 | 装甲布局 | 面对英国15" Mark I | | 水平防护的免疫区上限 | 50mm水平装甲(Wh)+80mm水平装甲(Wh) | 19,400m | | 混合区域的免疫区上限 | 145mm上部装甲带(KC)+80mm水平装甲(Wh) | 18,900m | | 同上，20度航向夹角 | 20,600m | | 同上，40度航向夹角 | 21,300m | | 垂直防护的免疫区下限 | 320mm装甲带(Wh)+110mm穹甲(Wh) | 21,000m | | 同上，20度航向夹角 | 10,000m | | 同上，40度航向夹角 | 0m | | 炮座防护的免疫区下限 | 340mm炮座装甲(KC)，不完整穿透 | 25,100m | | 同上，完整穿透 | 23,700m |
免疫区的计算范例：
德国海军认为英国15英寸舰炮能在21km以内距离上击穿俾斯麦级的320mm装甲带+110mm/68度倾斜的穹甲
查射表可知，其在21km上的落角约为21度，着速约为480m/s；查表面硬化装甲穿深曲线可知，在21度入射角下，完整击穿320mm表面硬化装甲所需的速度约为415m/s；查均质装甲穿深曲线可知，在47度入射角（90度-21度落角-22度装甲倾角）下，击穿110mm均质装甲所需的速度约为245m/s。
因此，总计穿速度=√(415²+245²)=482m/s，与480m/s左右的着速基本吻合。
德国海军认为英国15英寸舰炮能在19.4km以外距离上击穿俾斯麦级的50mm露天甲板+80mm装甲甲板
查射表可知，其在19.4km上的落角约为19度，着速约为490m/s；查均质装甲穿深曲线可知，在19度入射角下，击穿50mm均质装甲所需的速度约为235m/s，而击穿80mm均质装甲所需的速度则约为425m/s。
因此，总计穿速度=√(235²+425²)=486m/s，与490m/s左右的着速基本吻合。
美德两国算法的对比
按照德国海军的算法，去估算衣阿华级的免疫区数据：
在25,500码距离上，16英寸/45倍经火炮发射的2,700磅穿甲弹，落角为26.20度，着速为1,514英尺/秒，按照经验式（Ord. Sk. 78841）计算值，该角度下击穿1.5英寸水平装甲所需速度为555英尺/秒，击穿4.75英寸水平装甲所需速度为1258.5英尺/秒，击穿1.25英寸水平装甲所需速度为496英尺/秒，总计穿速度=√(555²+1258.5²+496²)=1,462英尺/秒
反推，按照经验式（Ord. Sk. 78841）计算值，在26.20度的落角，1,462英尺/秒的着速下，2,700磅穿甲弹可以击穿5.69英寸厚的水平装甲
在27,400码距离上，16英寸/50倍经火炮发射的2,700磅穿甲弹，落角为24.42度，着速为1,595英尺/秒，按照经验式（Ord. Sk. 78841）计算值，该角度下击穿1.5英寸水平装甲所需速度为582英尺/秒，击穿4.75英寸水平装甲所需速度为1335.5英尺/秒，击穿1.25英寸水平装甲所需速度为519.5英尺/秒，总计穿速度=√(582²+1335.5²+519.5²)=1,546.5英尺/秒
反推，按照经验式（Ord. Sk. 78841）计算值，在24.42度的落角，1,546.5英尺/秒的着速下，2,700磅穿甲弹可以击穿5.65英寸厚的水平装甲
基于以上情况来看，通过德国算法得出的数据与基于美国免疫区数据的反推算法得出的等效厚度相当接近，且同样与基于Sumrall书中记载的正推算法得出的等效厚度存在一定出入。
按照Sumrall书中记载的正推算法，去估算俾斯麦级的免疫区数据：
按照Sumrall书中记载的正推算法，俾斯麦级的水平防护等效厚度=50*0.5+80=105mm
德国海军认为英国15英寸舰炮能在19.4km以外距离上击穿俾斯麦级的50mm露天甲板+80mm装甲甲板
查射表可知，其在19.4km上的落角约为19度，着速约为490m/s，对照穿深曲线，约能击穿93mm的水平装甲。
可以看出，德国海军的算法，与Sumrall书中记载的正推算法同样存在一定出入。
结论
基于美国海军免疫区的反推算法，与德国海军的算法有一定的相同之处，而Sumrall书中记载的正推算法则与前两者都存在一定出入。 |
|
发表于 2014-8-24 22:41
楼主
发表于 2014-8-25 09:35
贴吧准入门槛太低，下限太低，继续待下去无意义了。
发表于 2014-8-25 22:44
