|
|
本帖最后由 seven_nana 于 2017-6-27 12:48 编辑
本帖内容未经允许不得转载
序言
本文旨在讨论美德两国的官方穿深计算方式，及其衍生出的数据中，所存在的异同点。
首先介绍一下本文的几个讨论对象：
一、Gkdos 100
全称为100/40 g.Kdos Unterlagen und Richtlinien zur Bestimmung der Hauptkampfentfernung und der Geschoßwahl，是德国海军所制定的一套火炮实战使用指南，其中包括了火炮的射表，穿深表，以及对典型目标各个部位装甲的穿透距离估算。
封皮
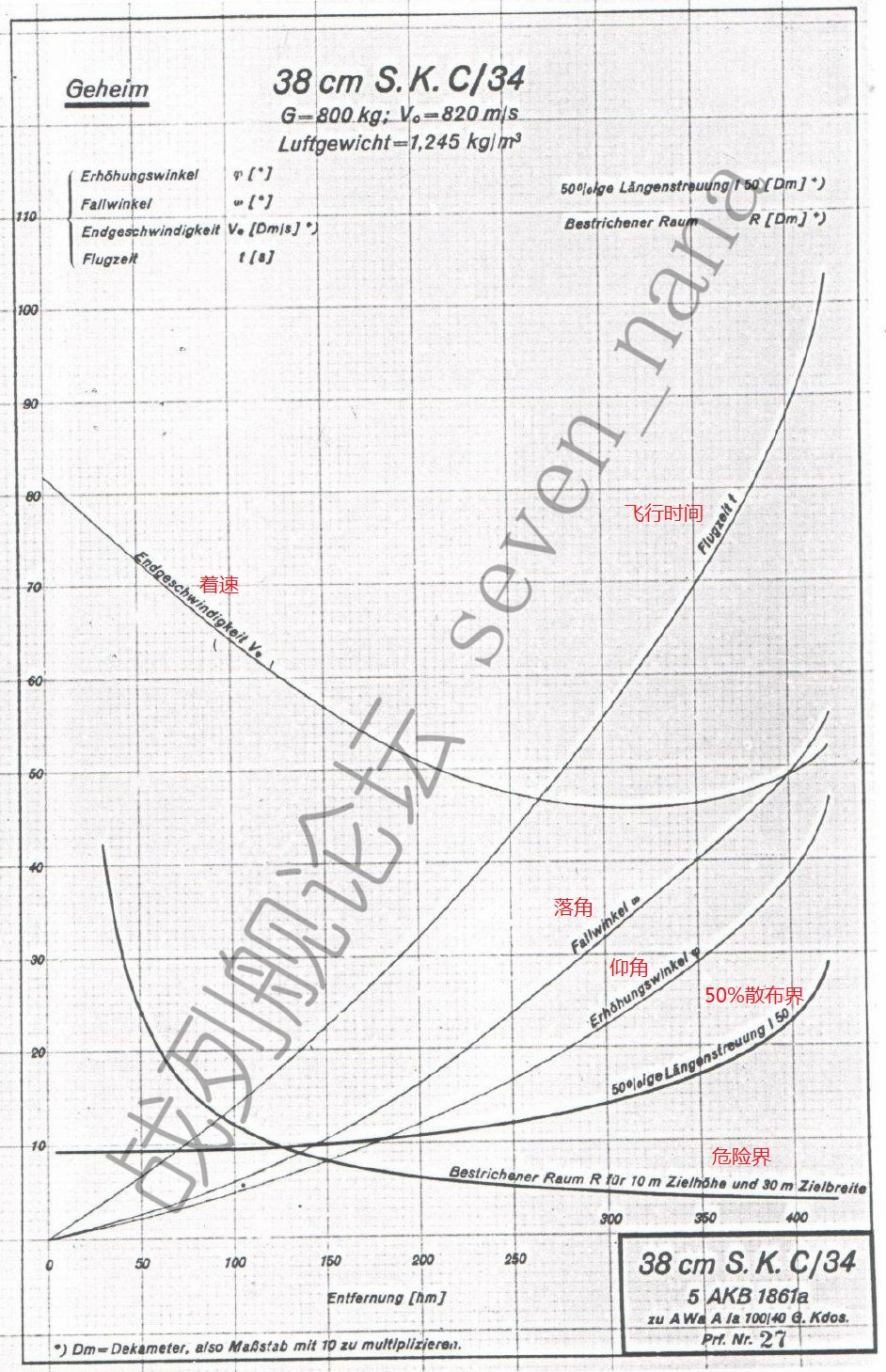
以下所列乃是38cm SK C/34的数据
射表
纵轴对应的单位，着速为10米/秒，危险界与散步界为10米，飞行时间为秒，仰角与落角为度。图表中的散布界实际上是50%散布界，即实际散布界的一半。图表中的危险界，对应的是高10米/宽30米的目标。横轴即射程，对应的单位为100米。
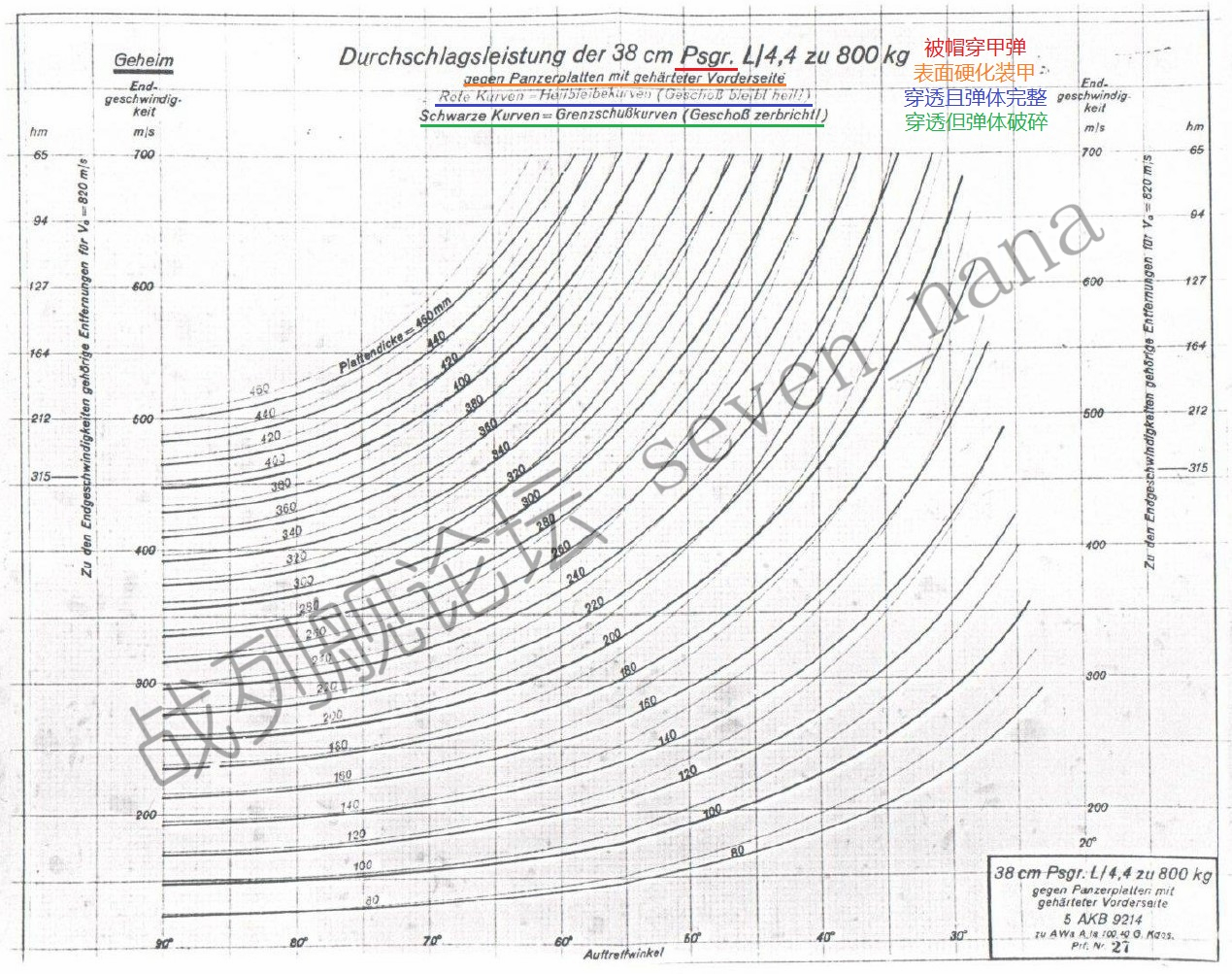
被帽穿甲弹对表面硬化装甲的穿深曲线
浅色线（原始图表中为红线）为穿透且弹体完整状态下的曲线，深色线（原始图表中为黑线）为穿透但弹体破碎状态下的曲线。
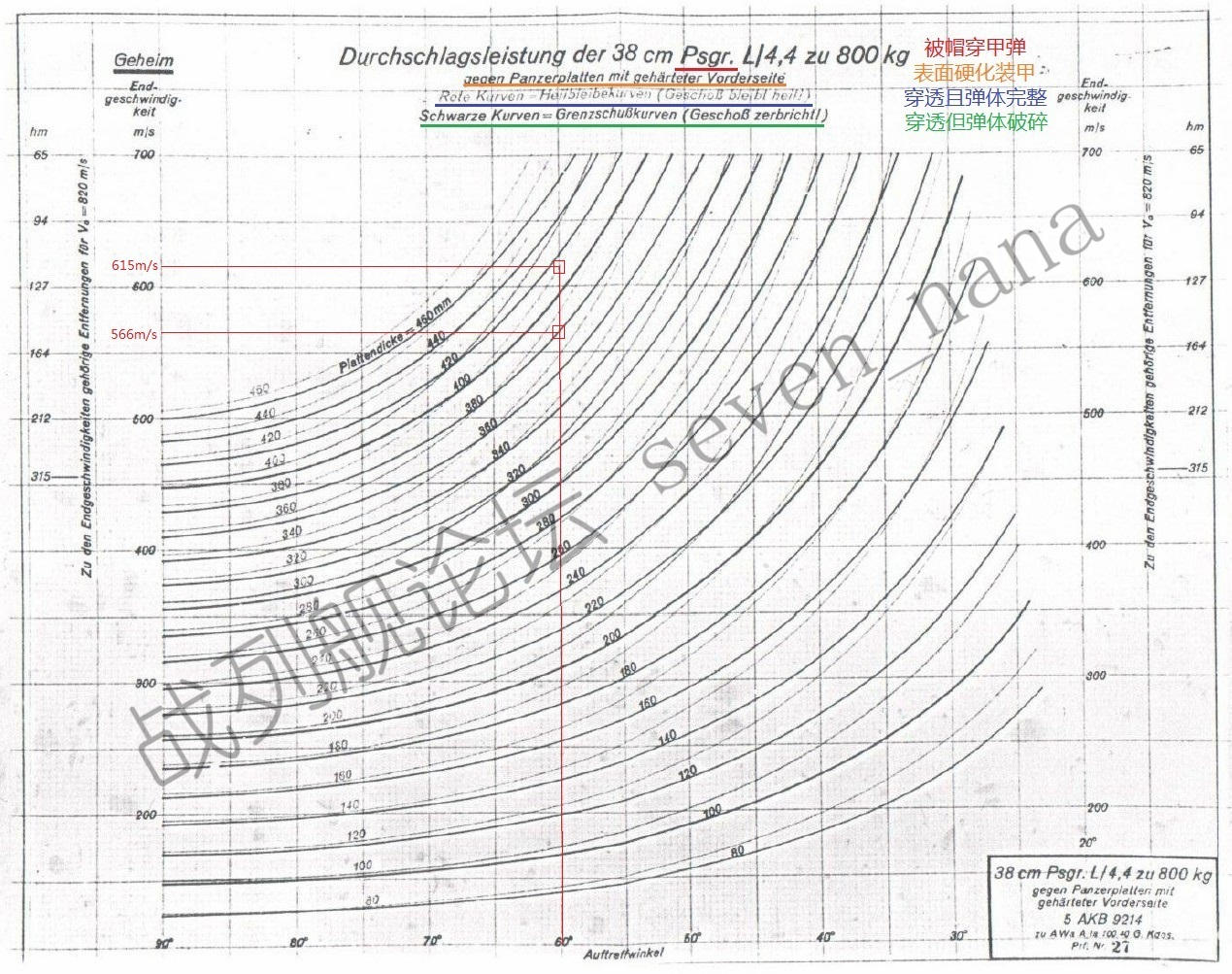
弹体完整穿透与弹体破损穿透的差异
由于表面硬化装甲具备嗑碎炮弹的能力，因此有时候尽管炮弹能够穿透装甲，但本身也会被嗑碎。由于这个缘故，在完整状态下击穿装甲，难度要比单纯的击穿装甲来得高一些。
以下图为例，如果对弹体状态没有要求，那么38cm穿甲弹只需566m/s的着速，便可在30度角下击穿380mm装甲；而若是要求弹体完整，则38cm穿甲弹需要615m/s的着速，才能在30度角下击穿380mm装甲。
被帽穿甲弹对均质装甲的穿深曲线
该曲线并未对弹体完整与弹体破碎两种状态加以区分。
二、NPG Report 5-47
全称为Naval Proving Ground Report No. 5-47, Ballistic Tests and Metallugical Examination of Japanese Heavy Armor Plate，是美国海军官方于1947年时发布的装甲测试报告，其中包含有美日德三国装甲的实测数据。
封皮
除了装甲测试数据外，这份报告中还提到了Ord. Sk. 78841公式。
Ord. Sk. 78841，全称Ordnance Sketch 78841，俗称“美国经验式”，是一种自1930年代起被美国海军正式采用的穿甲计算公式。
其具体公式为：
VL=（F×√e×d）/（41.57×√m×cosθ）
其中，F=6×（e/d-0.45）×（θ²+2000）+40000
VL=着速，e=装甲厚度，d=弹径，m=弹重，θ=倾斜角（垂直为0度，水平为90度）
在着速，弹径，弹重，倾斜角这四个参数已知的前提下，我们可以用反推的方式，计算出对应的穿深。
三、Ord-8
全称为Ordnance Phamhlet No. 8 Armor Quality, Test and Penetration，是美国海军官方于1923年时发布的穿甲相关的研究与数据手册。
封皮
在这份手册中，对美国海军当时采用的穿甲计算公式，即德玛尔公式进行了介绍。
Vd = 1022×(D^0.75×T^0.7)/P^0.5
V = 击穿速度，单位为英尺/秒
D = 弹径，单位为英寸
E = 装甲厚度，单位为英寸
P = 弹重，单位为磅
K = 德玛尔系数（用来调整公式结果，使其能与各类炮弹/装甲的实测数据相吻合的一个系数）
Mθ = 倾角调整系数（用来调整公式结果，使其能与不同倾角下的实测数据相吻合的一个系数）
讨论
通过对比这两个国家的穿深计算方式/结果，并结合其他的数据与资料，我打算对一下几个问题进行讨论：
一、倾斜装甲的抗弹效果
对于战列舰级别的倾斜装甲所具备的的抗弹能力，始终有部分人群抱有怀疑态度。有些将坦克级别的数据拿来与战列舰级别相提并论，另一些更是试图用三角函数来计算倾斜装甲的抗弹性能，这显然是贻笑大方了。
下面我将用美德两国的官方数据/算法，对此问题进行说明。
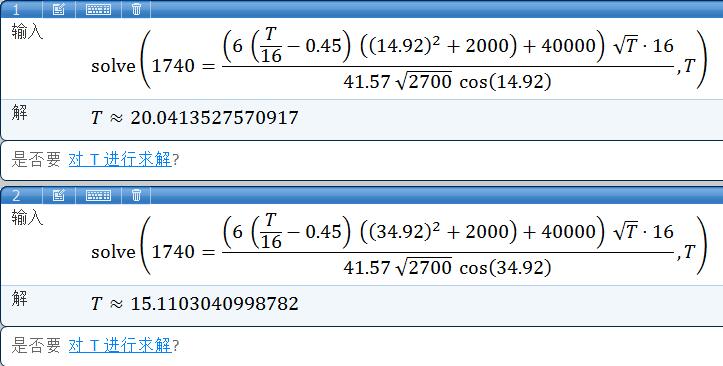
1930年代时的美国人的计算方式
在20,000码距离上，16英寸/50倍经 Mark 7型火炮的着速为1,740f/s，落角为14.92度。
鉴于20,000米是非常典型的交战距离，而美国16英寸/50倍经 Mark 7型火炮的弹道特性又较为中庸，既不太平直，也不太弯曲，相当具有代表性，因此我使用这组条件下的数据进行计算，并将其作为范例，来展示倾斜装甲的抗弹性能提升效果。
根据美国经验式的计算结果，该炮在上述距离上能够击穿20.04英寸的垂直布置的经验式装甲，或15.11英寸的20度倾斜布置的经验式装甲。换句话说，在上述条件下，20度倾斜布置的经验式装甲，其抗弹性能相当于1.32倍厚度的垂直布置的经验式装甲。
1940年代时的德国人的官方数据
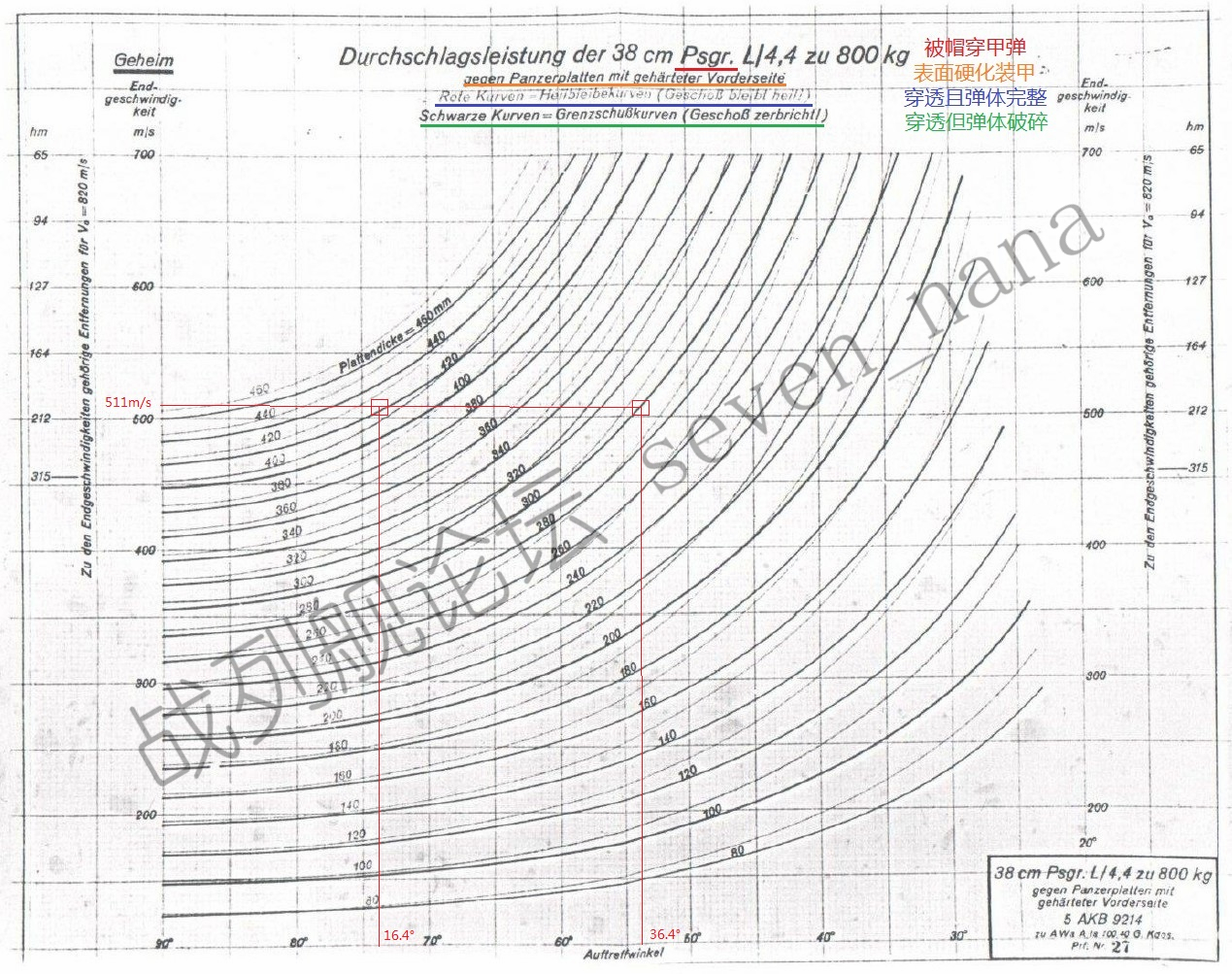
在20,000米上，38cm SK C/34火炮的着速为511m/s，落角为16.4度。
鉴于20,000米是非常典型的交战距离，而德国38cm SK C/34的弹道特性又较为中庸，既不太平直，也不太弯曲，相当具有代表性，因此我使用这组条件下的数据进行计算，并将其作为范例，来展示倾斜装甲的抗弹性能提升效果。
按照德国官方穿深表，在弹体完整的情况下，该炮在上述距离上能够击穿411mm的垂直布置的德国表面硬化装甲，或273mm的20度倾斜的德国表面硬化装甲。换句话说，在上述条件下，20度倾斜布置的德国表面硬化装甲，其抗弹性能相当于1.5倍厚度的垂直布置的德国表面硬化装甲。
结论：
无论是美国计算公式还是德国官方数据都能证明，20度倾斜布置的装甲，其抗弹性能会明显优于垂直布置的装甲。
注意：
为了保持同等的防护高度，倾斜装甲需要付出更大的重量代价。
面对不同落角的炮弹时，倾斜装甲的抗弹性能是不同的。通常来说，炮弹落角越大，倾斜装甲的抗弹性能也就越好。
一般来说，各类文章中提及倾斜装甲的等效厚度时，通常都是指在某个限定条件下的等效厚度。如美国快速战列舰的舷侧防护等效厚度，通常都是指其在免疫区下限距离上，面对对应火炮/炮弹时的等效厚度。
二、表面硬化装甲与均质装甲的抗弹性能差异
众所周知，出现于1893年（一说1894年）的克虏伯渗碳表面硬化装甲乃是装甲发展史上的一大里程碑。在随后的一甲子中，此类装甲及其后续改进版本始终是战列舰垂直防护装甲的标准用材。在面对无被帽的穿甲弹时，表面硬化装甲可提供远高于均质装甲的抗弹性能，这是由于表面硬化装甲上的硬化层能够有效破坏弹体结构，从而达到了削弱炮弹穿透能力的目的。
但甲弹发展的过程，乃是一个持续改进，螺旋上升的过程。在哈维硬化及克虏伯硬化装甲相继出现后，炮弹设计上也发生了技术跨越；在软被帽穿甲弹出现后，穿透克虏伯硬化装甲的目标已不再遥不可及；而当硬被帽穿甲弹出现后，更是让甲弹对抗的天平，再次倾向了炮弹一方。
因此，在面对不同类型的炮弹时，表面硬化装甲的抗弹性能表现会有较大的差异。在面对二战时期的最新型硬被帽穿甲弹时，甚至有可能连均质装甲都不如。
下面我便将采用美德两国的官方穿甲曲线及实测数据，对此问题进行说明。
1920年代时的美国人的官方数据
之前我们提到，美国海军在1920年代时使用德玛尔公式来评估穿甲效果，其中有两个很重要的参数，即K值与Mθ值。
为了便于实际计算，美国海军开展了一系列的实弹测试实验，并以此归纳出了当时技术条件下的K值与Mθ值。K值与Mθ值的乘积，相当于德玛尔公式的理论计算值与实弹射击得出的实际结果之间的换算系数。
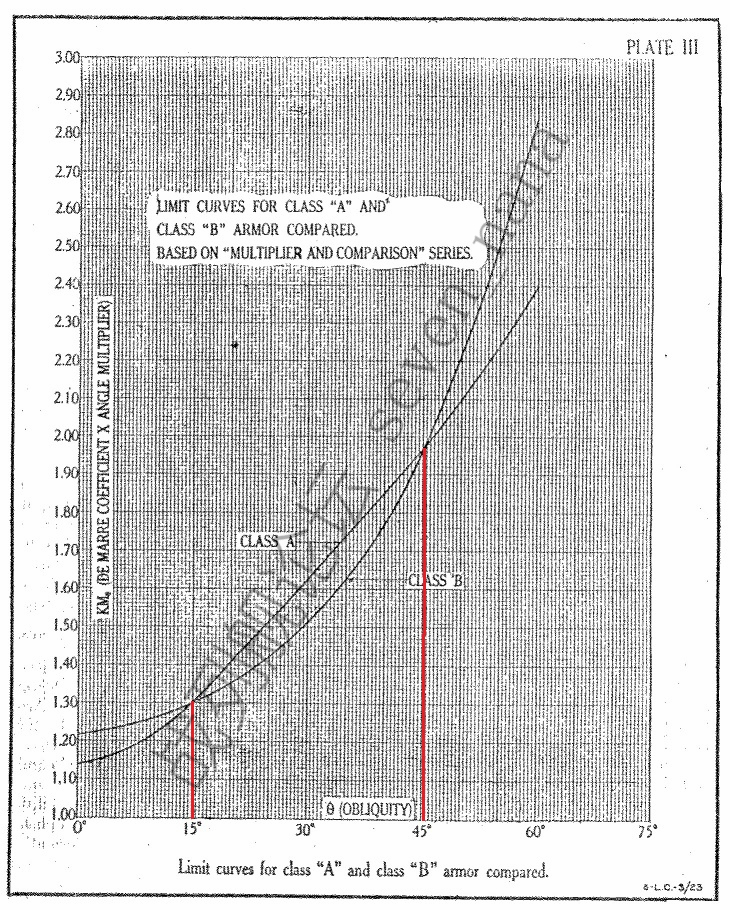
下图是美国人总结出的K值与Mθ值的乘积。
我们可以看到：在入射角小于15度时，Class B（均质装甲）的KMθ值高于Class A（表面硬化装甲）；在15-45度角下，Class A（表面硬化装甲）的KMθ值高于Class B（均质装甲）；在入射角大于45度角时，Class B（均质装甲）的KMθ值高于Class A（表面硬化装甲）。
换句话说，在入射角小于15度时，Class B（均质装甲）的抗弹能力优于Class A（表面硬化装甲）；在15-45度角下，Class A（表面硬化装甲）的抗弹能力优于Class B（均质装甲）；在入射角大于45度角时，Class B（均质装甲）的抗弹能力优于Class A（表面硬化装甲）。
除此之外，在这份研究档案中，美国人还列出了每一种火炮的穿深曲线。
美国8英寸穿甲弹（260磅）对Class A装甲
在15度入射角下，对7英寸Class A的弹道极限为1535f/s，对9英寸Class A的弹道极限则为1821f/s；在30度入射角下，对7英寸Class A的弹道极限为1915f/s，对9英寸Class A的弹道极限则为2288f/s；在45度入射角下，对7英寸Class A的弹道极限为2305f/s，对9英寸Class A的弹道极限则为2771f/s。
美国8英寸穿甲弹（260磅）对Class B装甲
在15度入射角下，对8英寸Class B的弹道极限为1677f/s；在30度入射角下，对8英寸Class B的弹道极限为1950f/s；在45度入射角下，对8英寸Class B的弹道极限为2516f/s。
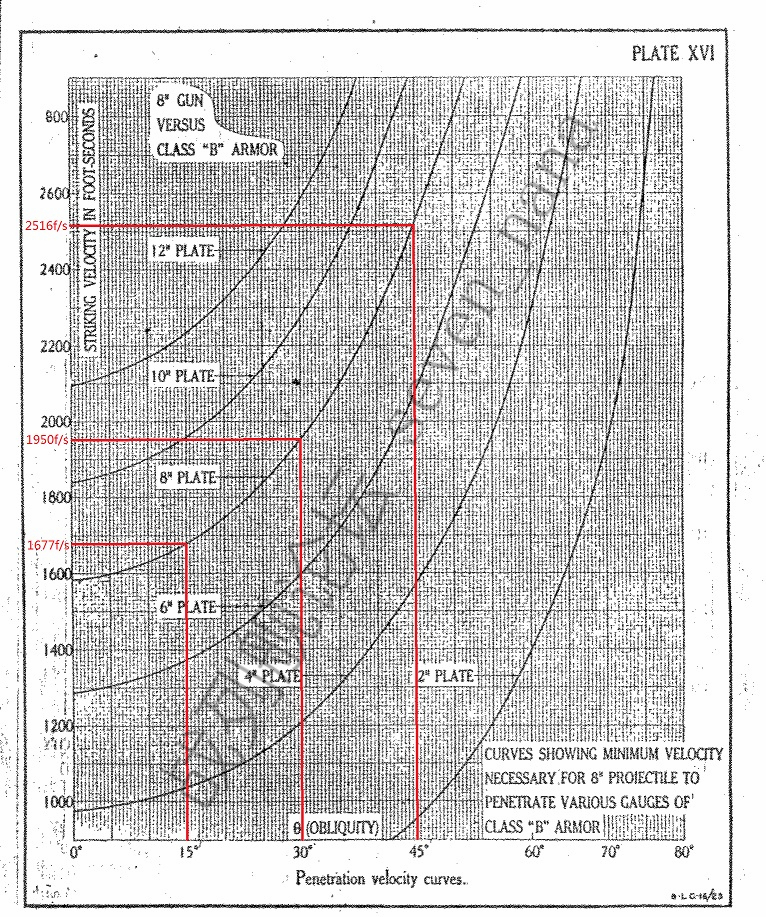
此外，仅凭目测便可确认，在0度入射角下，击穿Class A所需的最小速度，低于击穿Class B所需的最小速度。
数据分析：
鉴于这组数据中，没有面对8英寸Class B的弹道极限数据，故我将采用插值计算法，大致比较两种不同装甲的抗弹性能。
（1535+1821）/2=1678，1678/1677=1.0006；（1915+2288）2=2101.5，2101.5/1950=1.08；（2305+2771）/2=2538，2538/2516=1.009。
面对美国8英寸穿甲弹（260磅）时，在0度入射角下，Class A的抗弹性能逊于Class B；在15度入射角下，Class A的抗弹性能与Class B基本相当；在30度入射角下，Class A的抗弹性能显著优于Class B；在45度入射角下，Class A的抗弹性能与Class B基本相当。
美国16英寸穿甲弹（2,100磅）对Class A装甲
在15度入射角下，对15英寸Class A的弹道极限为1545f/s，对17英寸Class A的弹道极限则为1697f/s；在30度入射角下，对15英寸Class A的弹道极限为1929f/s，对17英寸Class A的弹道极限则为2106f/s；在45度入射角下，对15英寸Class A的弹道极限为2332f/s，对17英寸Class A的弹道极限则为2539f/s。
美国16英寸穿甲弹（2,100磅）对Class B装甲
在15度入射角下，对15英寸Class B的弹道极限为1545f/s，对17英寸Class B的弹道极限则为1689f/s；在30度入射角下，对15英寸Class B的弹道极限为1800f/s，对17英寸Class B的弹道极限则为1957f/s；在45度入射角下，对15英寸Class B的弹道极限为2342f/s，对17英寸Class B的弹道极限则为2544f/s。
此外，仅凭目测便可确认，在0度入射角下，击穿Class A所需的最小速度，低于击穿Class B所需的最小速度。
数据分析：
15寸组：1545/1545=1，1929/1800=1.072，2332/2342=0.996。
17寸组：1697/1689=1.005，2106/1957=1.076，2539/2544=0.998。
面对美国16英寸穿甲弹（2,100磅）时，在0度入射角下，Class A的抗弹性能逊于Class B；在15度入射角下，Class A的抗弹性能与Class B基本相当；在30度入射角下，Class A的抗弹性能显著优于Class B；在45度入射角下，Class A的抗弹性能与Class B基本相当。
结论：
对于1920年代初期的美国炮弹/装甲而言，在30度入射角下，Class A的抗弹性能要明显优于Class B；而在0度入射角下，Class A的抗弹性能则要逊于Class B；至于在15度与45度时，两者的性能则基本相当。因此总的来说，Class A的优势范围在于15-45度之间，以30度角附近为最佳；其余角度范围下则是Class B占优。
1940年代时的德国人的官方数据
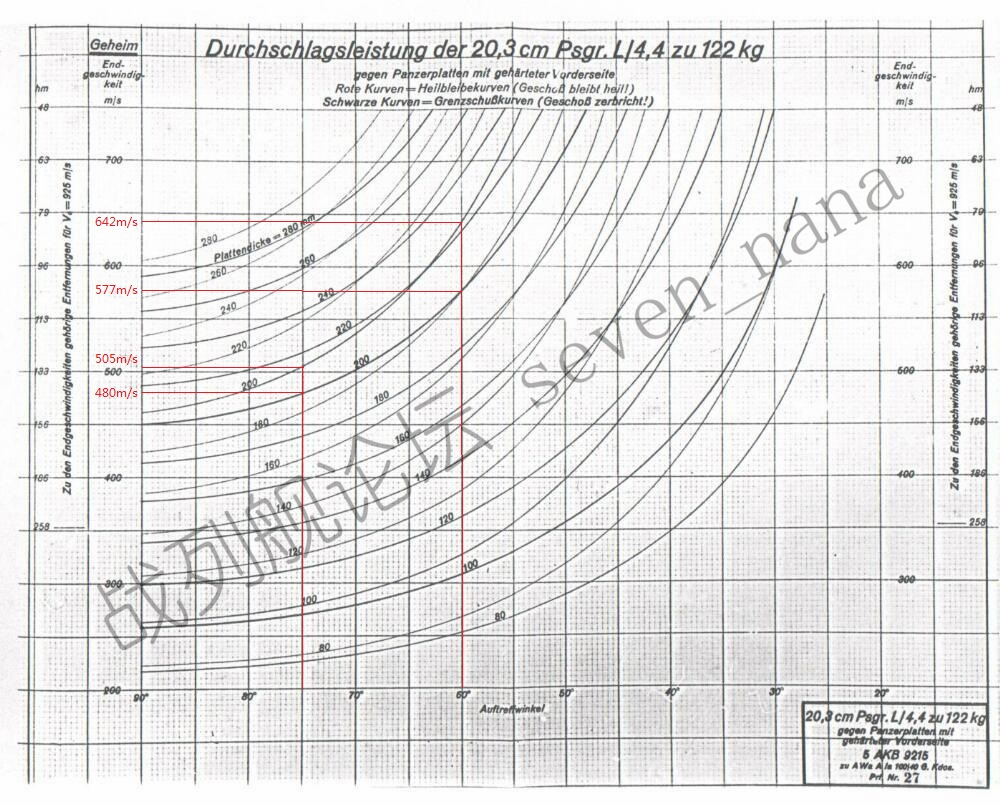
德国20.3cm穿甲弹对表面硬化装甲
在15度入射角下，对200mm的KC的弹道极限为480m/s（弹体破碎）或505m/s（弹体完整）；在30度入射角下，对200mm的KC的弹道极限为577m/s（弹体破碎）或642m/s（弹体完整）。
德国20.3cm穿甲弹对均质装甲
在15度入射角下，对200mm的Wh的弹道极限为500m/s；在30度入射角下，对200mm的Wh的弹道极限为617m/s。
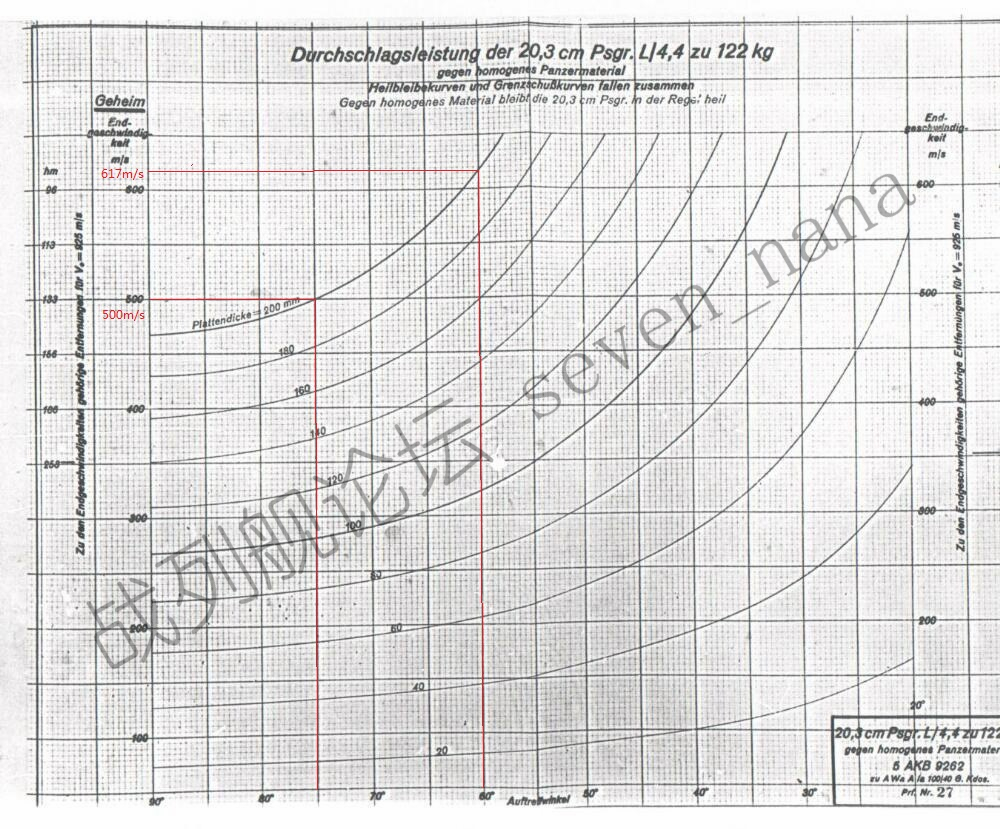
数据分析：
480<500<505；577<617<642。
此外，仅凭目测便可确认，在0度入射角下，以弹体破碎状态击穿KC所需的最小速度，低于击穿Wh所需的最小速度；而以弹体完整状态击穿KC所需的最小速度，与击穿Wh所需的最小速度基本相当。
结论：
在面对德国20.3cm穿甲弹时，在0度入射角下，KC的抗弹性能逊于Wh；在15度入射角下，KC的抗弹性能略逊于Wh；在30度入射角下，KC的抗弹性能与Wh基本相当。
1940年代时的美国人的官方数据
美国14寸Mark 16 Mod 8型穿甲弹（1,500磅），对Class A装甲
在30度入射角下，对13寸Class A（平均水准）的弹道极限为经验式弹道极限的89.7%。
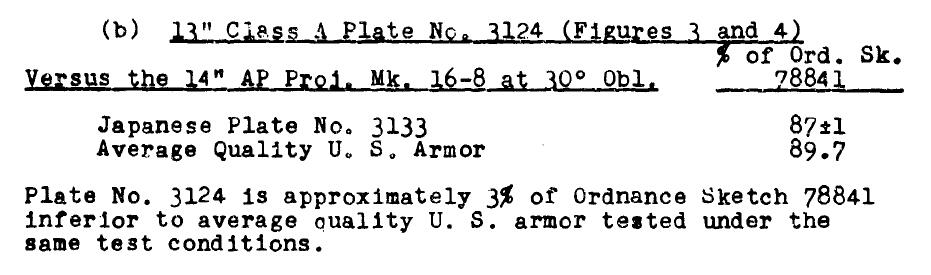
在30度入射角下，对15寸Class A（平均水准）的弹道极限为经验式弹道极限的89.6%。
美国14寸Mark 16 Mod 8型穿甲弹（1,500磅），对Class B装甲
在30度入射角下，对13.5寸Class B（平均水准）的弹道极限为经验式弹道极限的95.1%。
数据分析：
尽管这三组装甲的厚度各不相同，但鉴于13寸Class A与15寸Class A的相对得分如此接近，故我推测在13.5寸厚度上，Class A的相对得分在89%-90%之间，低于Class B的95.1%。
结论：
在面对美国14寸Mark 16 Mod 8型穿甲弹（1,500磅）时，在30度入射角下，Class A的抗弹性能显著逊于Class B。
补充说明：
根据已知资料：
1）在面对巡洋舰级别的炮弹时，德国均质装甲的抗弹性能与美国均质装甲大体相当，而在面对战列舰级别的炮弹时，不如美国均质装甲。
2）在面对巡洋舰级别的炮弹时，美国表面硬化装甲与德国表面硬化装甲大体相当，而在面对战列舰级别的炮弹时，不如德国表面硬化装甲。
3）在战列舰级别上，德国表面硬化装甲相对均质装甲的优势，会比巡洋舰级别上来的更大一些。
4）在巡洋舰级别上，美国表面硬化装甲部分夺回了对均质装甲的优势（至少在30度角左右时如此）。
以上结论均基于"Naval Proving Ground Report 5-47, Ballistic Tests and Metallugical Examination of Japanese Heavy Armor Plate"中的数据，鉴于这套数据已经发过多次，就不再重复发图了。
在战列舰级别上，上述两个不同时期的美国装甲的表现差异较大，这主要是由于两个原因造成的：
1）美国炮弹的被帽性能有所改善，使得表面硬化装甲的优势进一步降低了。
2）1920年代的美国主流Class A，基材厚度比例为65%；而二战时期的美国Class A，基材厚度比例仅为45%。
实际上美国人在表面硬化装甲的发展途径上，走上了一条错误的道路。美国人试图通过加大硬化层及过渡层比例的方式，强化对被帽及弹体的破坏能力；但这么做是有代价的，装甲的其他一些指标便受到了影响，因此最终呈现出来的整体抗弹效果很不理想。
总结：
对于间战时期的美国炮弹/装甲与二战时期的德国/美国炮弹/装甲而言，表面硬化装甲与均质装甲之间的抗弹性能差距并没有很大。总体来说，表面硬化装甲的优势范围还是集中在30度角左右，最大不超过15-45度这个范围；而在实战中，这也的确是表面硬化装甲最有可能面对的炮弹入射角范围。 |
|
发表于 2013-6-7 13:18
发表于 2013-6-9 07:35
楼主
发表于 2013-6-12 21:54
我也没有啊，我是看到okun去年写的NEW STS PLATE PENETRATION PROGRAM 里面提到过这三份新资料，看到你弄到了Ord 8和Gkdos 100这两份东西还以为你都找到了